Introduction
In previous blog, we learnt about artificial neurons and its types. This blog will illustrate those concepts with examples.
Now we are little bit familiar that how neural network learn using training data, so let's take this learning a bit further and do some exercise as our title says. So we will take some training data containing handwritten digits, considering those images will be segmented into single digit image and put those into our designed neural network for learning and then recognise the digits.
This will be done in two steps, in the first step we will design the network and second, will be the learning part.
Design the network
Before designing the network, we need to understand the architecture of neural network and what are its components.
Architecture of Network
Suppose we have the below network,
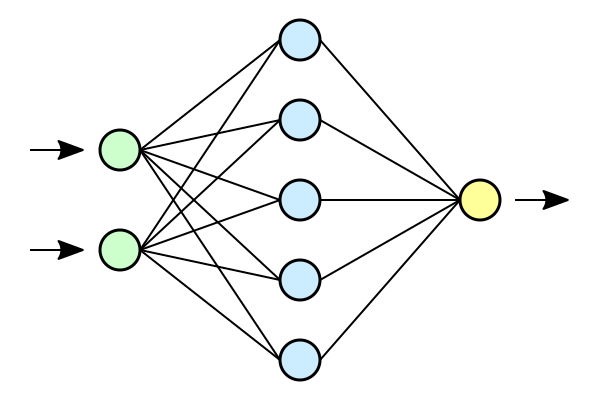
The leftmost layer in the network is called the input layer, and the neurons that are present in those layer are called input neurons. The rightmost layer in the network is called the output layer, and similarly neuron present in that layer is called output neuron or single output neuron. The middle layer is called a hidden layer, since the neurons in this layer can't be classified as inputs neither outputs, so called as hidden. Hidden layer can contain more than one layer within itself and those layers will also considered as hidden layers. These hidden layers takes inputs from input layer and generate output for output layer.
Generally, in neural networks, output from one layer is used as input to the next layer, such networks are called as feedforward neural networks. The information is always fed forward, never backward and no loops.
There are other models also, called as recurrent neural network. The neurons of this model fire for some limited duration of time, before becoming quiescent. These firing stimulate other neurons, which may fire a little while later, also for a limited duration. The effect is not instantaneous, that's why these don't cause problem.
Classifying Individual digits
We'll develop a neural network which can recognise individual digits from the training data.
For this, we will use a three-layer neural network:
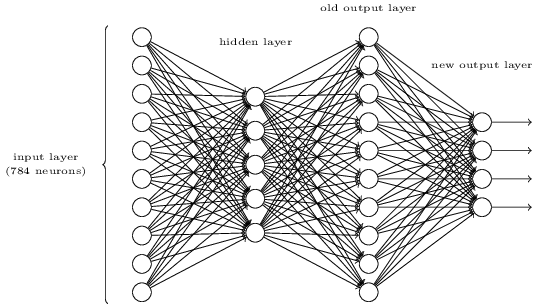
The input layer of the network contains neurons encoding the values of the input pixels. Each image containing digit is a 28 by 28 pixel image, and so the input layer contains 784 = 28 X 28 neurons. The input pixels are greyscale, with a value of 0.0 representing white, a value of 1 representing black, and in between values representing gradually darkening shades of grey.

The second layer of the network is a hidden layer. Let's denote the number of neurons in this hidden layer by n, and we'll keep experimenting with different values for n. For now, consider n = 15.
The output layer of the network contains 10 neurons. If the first neuron fires, i.e has an output = 1, then that will indicate that the network things the digits is a 0. If the second neuron fires then that will indicate that the network thinks the digit is a 1. And so on.
Up until now, the designing of neural network is done. Second step is to make this network learn to recognise digits.
Learning (with gradient descent)
We'll use MNIST data set as the training set for the network. MNIST contains thousands of scanned images of handwritten digits, together with their correct classifications.
Note : we have to divide the data into 3 sets which are Training set(70%), Tuning/Validation Set (10-15%) and Test set(10-15%). We can discuss about this 3 set rule in detail in coming blogs.
Let's denote the training input as \(x\), and we'll denote the desired output by \(y = y(x)\), where y is a 10-dimensional vector. For example, if a particular training image depicts a 2, then \( y(x) = (0,0,1,0,0,0,0,0,0,0)^T \) is the desired output from the network. Here T is the transpose operation, turning a row vector into a column vector.
Our goal is to derive an algorithm which let us find weights and biases so that output from the network approximates \( y(x) \) for all training inputs \( x \). To achieve that goal we will define a cost function, A cost function is used to determine the difference between the actual values and predicted values and measure how wrong our network or model in prediction or in this case determining the correct output.
This is an iterative process. Machines learns and tuned by iteration.
Cost function defines as,
\( C(w,b) \equiv \frac{1}{2n} \sum_{x} || y(x) - a ||^2 \)
Here, \(w\) denotes the collection of weights in the network, \(b\) all the biases, \(n\) is the total number of training inputs, \(a\) is the vector of outputs from the network when \(x\) is the input and the sum over all the training inputs.
Since cost function is used to determine the difference between actual and predicted values, but we are expecting that to perform with good accuracy. So we need to minimise the difference of that value between actual and predicted in order to get optimal results.
That was theoretical, let's understand using the function.
\( C(w,b) \equiv \frac{1}{2n} \sum_{x} || y(x) - a ||^2 \), here as we see that \(C(w,b)\) is non-negative, since every term in the sum is non-negative. Furthermore, the cost \(C(w,b)\) becomes small, \(C(w,b) \approx 0\) when \(y(x) \approx a\) for all training inputs, \(x\), that means our Training algorithm did a good job if we could find weights and biases so that \(C(w,b) \approx 0\). Also training model is not doing well when \(C(w,b)\) is large. Hence we need to minimise the cost \(C(w,b)\) as much as possible by finding a set of weights and biases.
We'll obtain that by using algorithm known as gradient descent.
Gradient Descent is an optimisation algorithm which is commonly used to train machine learning models and neural networks. There's an article by IBM regarding this you can read to have a detail knowledge on this topic.
Gradient descent works extremely well in neural networks and to minimise the cost function, hence help the network to learn.
However, We're not going to see whole calculas behind the minimisation of cost function, rather we'll implement directly using some code and machine learning tools.
This is it for the concept part. Next, we will see the actual implementation through coding.
How cost function is derived to find its minimum using gradient descent, you can check this in detail by book written by Michael Nielsen on Neural Networks and Deep Learning. He has explained the whole concept with depth and worth a read.
Thanks for reading.
Until Then,
Keep Building Yourself 🦾
Cover Photo by Markus Krisetya on Unsplash

