Why Neural Network

Today, Neural network is playing a major role to train machines for Image Recognition, Natural Language Processing, Computer Vision and many more which human brain do effortlessly because we carry a supercomputer in our heads and training our brains with tons of data since ages. It's a very unnoticeable power of humans that how easily we're able to understand things which are captured by our eyes, and we don't really appreciate our brains that it does such complex image processing progressively with the help of visual cortices containing millions of neurons connected with other billions of neurons.

We already know that it really easy for humans, but what about machines how is it possible for machines to achieve that level of perfection like humans. Let's say if we want to write a computer program to recognise handwritten digits written with 1000s of different style of handwritings, I guess it'll be pretty impossible to achieve it algorithmically.

For such problems, Neural networks have different approaches to understand handwritten digits. It uses training data to automatically infer rules for recognising handwritten digits and as much we increase the amount of training data, its accuracy will also increase.

How neural network does this ?

To understand this, we need to be aware of aritificial neurons and some standard learning algorithms of neural networks. In this blog, I'll only focus on aritificial neurons and in the next we'll tackle the algorithms.

Artificial Neurons

Neural network is a simplified model of the way the human brain processes information. The basic units are neurons, which are typically organized into layers. Just like human brain, machines have artificial neurons.

In neural network, artificial neuron is a model containing mathematical functions which produces outputs and inputs for other layers inside the network.

Below image is of a single artificial neuron which takes \(X1, X2,.....,Xn\) as inputs and produces Y as output.

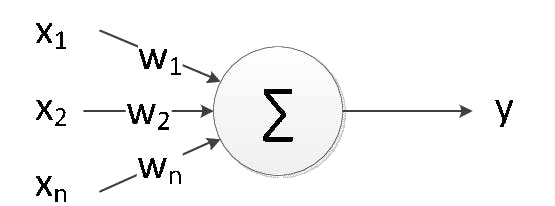
To start with, we have two important artificial neurons to understand first, Perceptron and Sigmoid.

Perceptron Neuron

A perceptron neuron takes serveral binary inputs, \(X1, X2,....Xn,\) and produces a single binary output as shown in the above image as well.

But you might have noticed along with X as inputs there are \(W(W1, W2, .... Wn)\) are also going for the computation. So after the work by Warren McCulloch and Walter Pitts on first artificial neuron, scientist Frank Rosenblatt in 1960s proposed a simple rule to compute the output. He introduced weights, \( W1, W2,..Wn, \) real numbers expressing the importance of the respective inputs to the output. The neuron's output, 0 or 1, is determined by whether the weighted sum \( Wn.Xn \) is less than or greater than some threshold value. Just like the weights, the threshold is a real number which is a parameter of the neuron.

How does it works

Let's understand this with an example, Suppose you're on a date with someone and went to a cafe, trying to initiate the conversation but don't know on which topic you'll start so that you won't embarrass yourself and at the same time you want to impress that person and want some positive feedback after the date. You know what I mean.

Ok ! I think from the above conditions you might have clearly identified that our output is to impress that person. So since our results would be in binary representation, simplifying our condition, we will have,

0, if Not Impressed
1, if Impressed

Then, What are the inputs ? Answer is, input depend on you that how you want to impress that person. So this is like trial and error method in the layman terms but in neural network this is called training data.

You'll try to impress that person with lots of things and then look for the reaction from her/him and then adjust the weightage of each thing randomly to know, in which thing she/he looks more interested.

So, let's take some 3 common inputs,

• \(X1\), If you are already aware of the cafe, then may be you'll start talking about the cafe, its interior, food, service etc
• \(X2\), Then, may be about movies
• \(X3\), Also, you're bad at jokes but still trying to be funnier with some lame jokes to impress.

and now since we have inputs, according to perceptron model we assigned some weights on each inputs, let's say 5 for the first one, 2 for second, 3 for third. Considering that you're fond of that cafe that's why giving maximum weightage to the first input. Finally, suppose you choose a threshold value of perceptron as 5.

With above inputs and weights, perceptron implements the desired output, where for each topic if he/she looks interested then output is 1, and if not then 0. Through the time you came to know that person seems interested in movies, and other talks doesn't matter or interest that person. So if you talk about movies, the person will seem interested and may be you might impress him/her so it outputs 1, and if you talk about other topics you'll get output as 0. But since you gave more weightage to talk about cafe so you might not receive a good feedback about the date.

after putting everything together, the final output could be determined as,

0 if weighted sum \(Xn.Wn\) less than or greater than threshold value, 1 if weighted sum \(Xn.Wn\) greater than threshold value

Like this, by varying weights and threshold value, you'll get different results of your date.

It might not be the best example to demonstrate how perceptron model works but what I'm trying to explain here is, how perceptron adjust weights for each inputs to make desired outputs. Since, end result will be either 0 or 1, it means a single output, that means it must be working in a complex layer structure of networks to achieve that to sum up all the different inputs and outputs together.

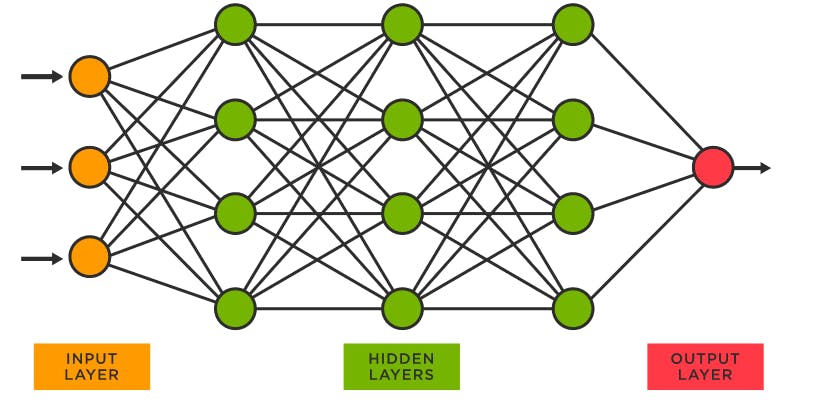
Layers of the network

Clearly, the first columns/layer of perceptrons contains all the inputs and weights. Then to level up for complex calculations or decisions, those outputs from the first layer become the input for second layer, which is often called hidden layer. There could be many layer between first and final layer which are considered as hidden layer. And then we have the final output layer which may contain more complex calculations or decision making capabilities which will give us the final output.

Visually it looks like this,

Problem with Perceptrons

You might have noticed that it takes binary input and produces output as 0 or 1, so when you assign weights for any of the inputs and final output seems incorrect or not what we wanted, so we will adjust adjust weights according to reach to that correct/desired output. But it would be very cumbersome to adjust weights for a long range of inputs also We won't know how far we are to reach the correct output.

When the network contains perceptron, a small change in the weights of any single perceptron can sometimes can make the whole network complicated and if any layer outputs wrong results it can change the final result as well and very hard to control in the way. Also its hard to identify where we are applying wrong weights and the network might not learn properly that what its purpose.

But, We can overcome this problem by using another type of artificial neuron called sigmoid neuron.

Sigmoid Neuron

Sigmoid neurons are similar to perceptrons, but modified so that small changes in their weights and thresholds cause only a small change in their output. That's the crucial fact which allow a network of sigmoid neurons to learn.

Just like a perceptron, the sigmoid neuron has inputs \( X1, X2,...Xn\), but instead of taking inputs 0 or 1, it takes any values between 0 and 1, which means 0.4 or 0.8 are some valid inputs. Also just like a perceptron, the sigmoid neuron has weights for each input, and overall bias, b. Bias is similar to threshold. Also it doesn't produces output as 0 or 1. Instead, Sigmoid neuron produces output using a function called, sigmoid function, which is defined as below,

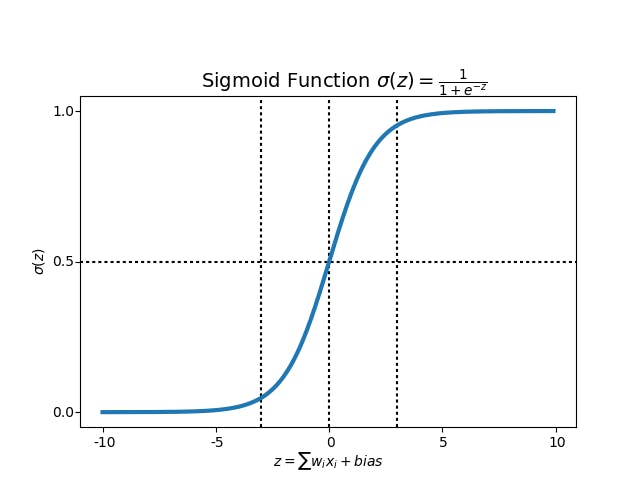
In the image you might have noticed a logarithmic function, you may or may not be familiar with but we'll deeply dive into sigmoid function with some exercise in the next blog.

For the basic level of understanding, sigmoid neurons in the network help that network to learn with more accuracy and produces efficient results.

In the next blog, I'll try to demonstrate sigmoid model with some exercises.

Stay Tuned & Thanks for reading !

Til Then,

Keep Building Yourself